

韓雄:問題導學法在高中數學教學中的應用
時間:2022-09-29 來源:
問題導學法在高中數學教學中的應用
成都冠城實驗學校 韓 雄
數學知識具備高邏輯性與抽象性,許多學生步入高中后認為高中數學知識,相比初中而言,更加抽象與深奧,學習難度明顯加大。學生在面對難度大的數學知識的學習過程中,如果得不到正確的引導與正確學習能力的培養,很容易因學習受挫,屢戰屢敗而影響學習數學的積極性,甚至影響到學生自主學習、探究、合作能力的培養,不利于個人素養的提升,也不利于實現個人的全面發展。
一、深度學習下的問題導學法應用于高中數學教學的意義
以學生為主體,以教師為主導,以探究為主線,體現與培養了學生的能力與學科素養。高中數學教學結合問題導學法,是借鑒國內流行的教學方式,結合高中數學學科特點與教學實際,通過吸收、借鑒、改造與創新而成的教學方法。開展此教學模式的課堂教學活動,教師引導學生始終圍繞問題進行,問題既是開端也是終點。整個過程在提出問題——探究問題——解決問題——生成新問題——探究新問題……模式中呈螺旋式循環過程。高中數學教學內容以此種形式,將深奧難懂的數學知識通過一個個小問題讓學生主動參與,積極探究,在不斷探究問題與新問題的過程中,降低了學生學習更加深奧、抽象的高中數學的難度,實現新知識的掌握與數學學習能力的培養,促進了學生對知識的深度思考。
二、深度學習下的問題導學法在高中數學教學中的實際應用策略
(一)問題的課前導入
高中數學教師要善于將數學教學目標轉化為問題,設置的課前導入問題緊扣本節課的教學目標,以恰到好處的時機、難度與提問方式,提出具有思考深度,適合學生與教材的探究性問題。比如單元復習在教學中占有很重要的地位,這是因為,在一個章節結束后,通常要把零散的知識“串聯”起來,形成“邏輯連貫”的有機整體,而這種“串聯”的方式就是單元復習。但在實際教學中,有時限于種種原因,單元復習做得比較匆忙,甚至沒有做,如有時是知識清單的低層次簡單羅列,思想方法總結不到位,典型題沒有總結與歸納,更沒有變式與拓展,導致學生思維不深刻,無法觸發學生的高效學習、深度學習等。筆者以人教版高一數學必修四第一章《三角函數》單元復習課為例:
學習任務1(自學)
問題1:任意角和弧度制、任意角的三角函數的概念分別是什么?
問題2:三角函數的六個誘導公式是什么?請簡要概括公式一到四,公式五和六的特點?
問題3:畫三角函數的圖像時應抓住哪幾個關鍵點?三角函數的性質有哪些?
問題4:函數圖像的伸縮變換是怎樣實現的?請舉例說明?
在上課之前,班上學生自己歸納、總結,得出本章的知識框圖,并在導學案上對題干進行設問、變式及解答(課前,分小組合作,老師布置任務并加以引導)。因為這幾個問題對于高中生來說都是很容易回答出來的問題,同學們在整理過程中開始主動思考,并且此類簡單問題的回答也為學生學習構建本章知識網絡建立起了基本的自信心。
(二)課中結合教材與學生情況進行分層提問并重視合作探究
結合教材是為了不偏離教學目標。結合學生情況時尊重學生主體地位,根據學生對知識的理解與吸收進行提問,避免問題難度過高挫傷學習積極性,或難度過低沒有挑戰性降低學生回答正確后的成就感。分層提問的重要性在于,由淺入深,一步步引導學生逐步建立起學習知識的自信心,并在問題的步步引導中讓學生在不知不覺間實現對知識體系的完整掌握。
以下面這節復習課為例:
1.老師引入課題,展示學生整理的知識框圖,學生分小組討論并評價所展示的知識框圖的優缺點,不足之處用彩筆修改、呈現。

2.根據學生的發言與討論,教師要引導學生歸納復習一章知識的流程與要求是什么,老師給出一個示范的知識流程圖:
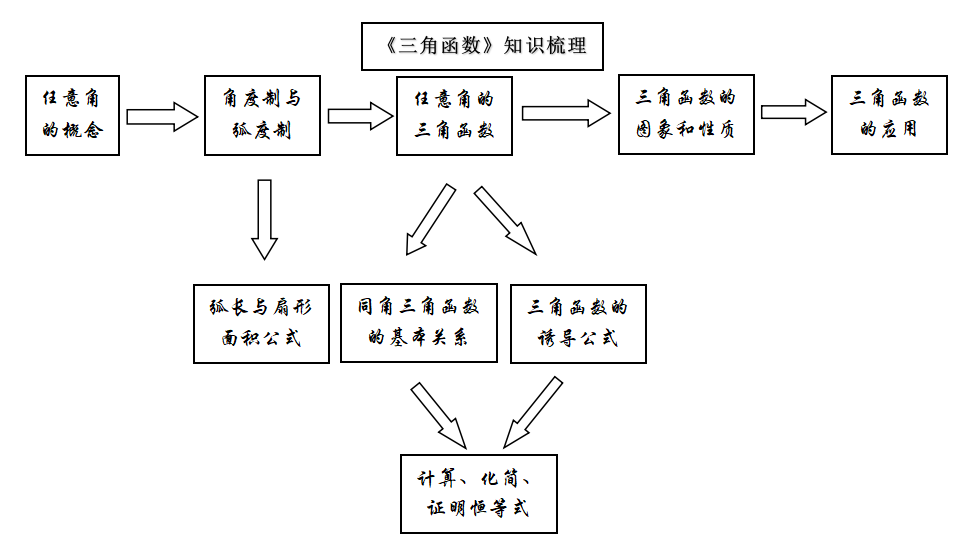
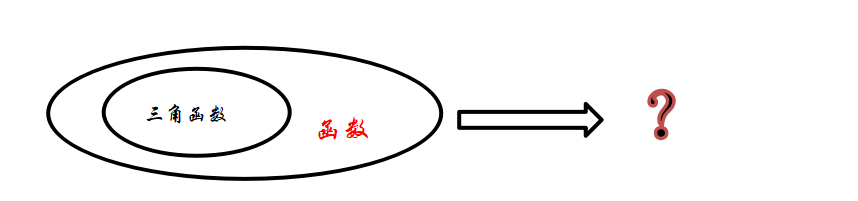
在這個過程中,老師和學生通過知識點、線、面復習完本周知識,繼續引導學生進行深度思考三角函數是函數范疇,繼續拓展函數的知識結構,這個過程增加了學生學習的深度。一個重要的發現,那就是學習內容自身并不需要很大的難度,關鍵在于學習內容能否促進學生深入思考。深度學習要緊扣思維來進行,在實際教學中,教師在設計教學的時候,固然要思考教學內容,但更要研究學生,尤其是學生的思維起點,即使實施深度學習,也可以結合最近發展區來考慮,判斷學生思維有可能到達的高度,然后去實施深度學習,效果會更加理想。
3.學生根據老師的布置,在回顧本章知識點及作業后,對一個題干自己設問及變式,其它小組解答。在原有的題干上讓學生進行設問及解答,學生就會開始主動思考并探究怎樣設計問題,從出題者角度去審視知識點,學生學習的主動性與積極性明顯增強。整過過程采用小組合作,讓學生在組內通過互相討論,對自己設計的問題進行優化,并讓其它小組解答提出疑問。由于是小組學生相互討論出的結果,也加強了學生的合作意識與團隊精神的培養。整個過程學生都主動進行了課前預習,上交了各自搜集的有關材料,積極性與主動思考的習慣在第二次課中實現了延續。
學生深度學習的關鍵在于學生思維的深度,而思維的深度又需要情境與問題來保證,只要學生在問題中思維深入了,那深度學習就發生了,核心素養的培育也就會成為現實。
4.在問題中穿插變式教學
高中數學知識要通過“練”來掌握,只要訓練量足夠,對學生打好基礎、掌握解決問題的能力,無疑是一種有效的方法,但這種做法學生需要花更多時間去完成一定數量的題目,學生才能理解,這會導致負擔過重,產生思維定勢,學生必然缺乏數學的創新精神。對優秀學生來說,大量重復的練習不僅會耗費學習時間,還不容易發展數學思維,而且容易造成數學厭倦,所以我們必須要采取課堂教學變革。針對一個知識點,圍繞這個知識點進行變式的問題教學,變式設計問題與知識點緊密相關,通過變式的問題教學,揭示知識點背后演繹的數學思想方法,從而達成知識點教學目標的實現。比如高中數學中“軸對稱與點對稱”這個知識點,進行如下問題變式導學:
問題一:復習奇偶函數的定義


從這個問題教學中,讓學生從奇偶函數的圖像具有對稱性,一步一步發散到軸對稱與點對稱的知識點,然后得到軸對稱的實質是中點和垂直關系的應用,點對稱的實質是中點坐標公式的應用,這樣問題變式教學不僅所需要的時間較少,做的題也不多,學生很快就掌握了知識的本質及內在聯系。在高中數學教學中,深度學習往往體現在數學知識的運用上,數學知識的應用一般有兩類:一是同類情境的直接運用,二是間接思路下的變式應用,相比較而言,后者更能體現深度學習。
深度學習下的問題導學法尊重了學生的主體地位,也充分發揮了教師的主導作用。其以提出問題為導向,以解決問題為表層目的,以培養學生獨立思考能力與自主學習能力實現全面發展為深層目的。深度學習的本質是學生內在階梯式的學習方法,更加突出高階思維的培養和構建,最終通過形成數學素養提升而影響學生的發展,從而實現有意義的學習和數學知識的自我構建,發展學生的數學核心素養。
(作者系成都冠城實驗學校教師,該文發表于《課程教育研究》2020年第12期)